About Pendulums
Simple Gravity Pendulum
A so-called "simple pendulum" is an idealization of a "real pendulum" but in an isolated system using the following assumptions:
- The rod or cord on which the bob swings is massless, inextensible and always remains taut
- The bob is a point mass
- Motion occurs only in two dimensions, i.e. the bob does not trace an ellipse but an arc.
- The motion does not lose energy to friction or air resistance.
The differential equation which represents the motion of a simple pendulum is
 is acceleration due to gravity,
is acceleration due to gravity, 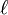 is the length of the pendulum, and
is the length of the pendulum, and  is the angular displacement.
is the angular displacement.Part One
The apparatus of the first part of the experiment involves two ring stands, with a knife edge attached horizontally. The knife edge is used to hold up the ring that is concaved to half its thickness at a part of the inner side. There is another ring stand, with a photogate attached. Tape is attached to the ring so that the photogate can detect the position of the ring. The photogate measures how much time it takes for the physical pendulum to pass the photogate twice. This relates to the period of the pendulum, where it reaches the amplitude in the positive and negative direction from equilibrium and reaches equilibrium. A computer with LoggerPro was also needed to collect the data from the photogate and provide the period of the system.
First, the moment of inertia of the ring was obtained using the following calculation
And then we took the expression and force it to look like "alpha = - ( ) sin theta"
Within the ( ) we are able to obtain our predicted period.
Next, the actual experiment was performed where the ring was oscillated at small angles, and the experimental period was measured by the photogate. Once the equipment was set up as shown in the apparatus, the experiment was performed, and the result is shown below
The experimental period of the physical pendulum with the ring was found to be 0.720 seconds. The percent error of the period of this physical pendulum was calculated

As can be seen, the percent error in this part of the experiment is very small, indicating that the theoretical period is the true period. It also shows that the assumption that when the angle is small, sin theta is almost equal to theta is also a good assumption. Lastly, it also shows that the method used to obtain the period is also accurate and correct.
Part Two
The second apparatus of this experiment involves the same setup, except that different physical pendulums are attached. A semicircle by the center of its diameter was pivoted, and it was also pivoted for a second trial by the highest tip of the curve.

First, the center of mass of the semicircle pendulum was obtained, using the procedure shown below
Picking dm as a strip of the semicircle, the center of mass in the x direction was zero, based on an origin in the center of the diameter. The center of mass in the y direction was found to be 4R/3pi.
Next, the moments of inertia of the semicircle about the center of the diameter, the center of mass, and the tip of the curve were obtained, using the same procedure as in part 1.
Using semicircular shells, the moment of inertia of the semicircle was found to be 1/2MR^2. Next, the moment of inertia of the semicircle at a pivot at the center of mass was found using the parallel axis theorem, and its derivation is found below

Lastly, the moment of inertia at the tip of the curve of the semicircle was found using the parallel axis theorem again.

Then, using the derived moments of inertia, the periods for the semicircle pendulum oscillating about the center of the diameter and the tip of the rim were calculated, as shown below

The same was performed for the semicircle oscillating about the highest tip of the rim.

Next, the shapes were measured and cut out from foam, and the actual experiment was performed, as in part 1, and the actual periods were obtained. The period found for the pendulum about its center of diameter is shown below

Again, the period is shown below for the pendulum about the tip of the rim

The percent error between the actual and theoretical values for the period of oscillation about the center of diameter was found to be 4.8%. Likewise, the percent error for the the period of oscillation about the tip of the rim was calculated as -4.7%. The percent error is high for a system such as a physical pendulum. These high percent errors, along with the percent error of the first part, show that the errors in this experiment are resulting from human error, and not error from the path taken to calculate the theoretical values and the procedure used.
Conclusion
Part One
One reason that the experimental period value is slightly larger than the theoretical is due to uncertainties in the measurements of the dimensions of the ring. In addition, there is also uncertainty in the measurement of the period by the photogate. Also, some friction is present in the pivot where the ring is in contact with the knife edge, lowering the angular frequency by a little and resulting in a higher frequency. Lastly, air resistance as the pendulum is oscillating can result in a slower angular velocity and a larger period. As can be seen though, because the percent error is very small, these errors and uncertainties have little effect on the system.
Part Two
The reason for such a high percent error is that, due to the lack of time, the physical pendulums were not pivoted correctly, resulting in the wobbling of the pendulums and movement back and forth, instead of only side to side movement like a regular pendulum. In addition, there was some noticeable friction at the pivots, resulting in the physical pendulums slowing down over time during the experimental gathering of data. To make this experiment better, better pivots should be used for the semicircle pendulums that does not result in the wobbling of the pendulums, and more time would be needed to perfect the experiment. Lastly, more dense material should be used for the pendulums instead of foam), giving the pendulums more control during the oscillations.















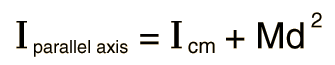























 or
or 















 &
& 
 of the disk is 7.04 rad/s. Calculating
of the disk is 7.04 rad/s. Calculating 
